Gauss Jordan Elimination Method

By Yin_74Darren 23 Aug, 2022 Post a Comment

The gauss Jordan calculator reduces the. The process of row reducing until the matrix is reduced is sometimes referred to as GaussJordan elimination.

Gauss Jordan Elimination Reduced Row Echelon Form Youtube

Use row operations to transform the augmented matrix in the form described below which is called the reduced row echelon form RREF.

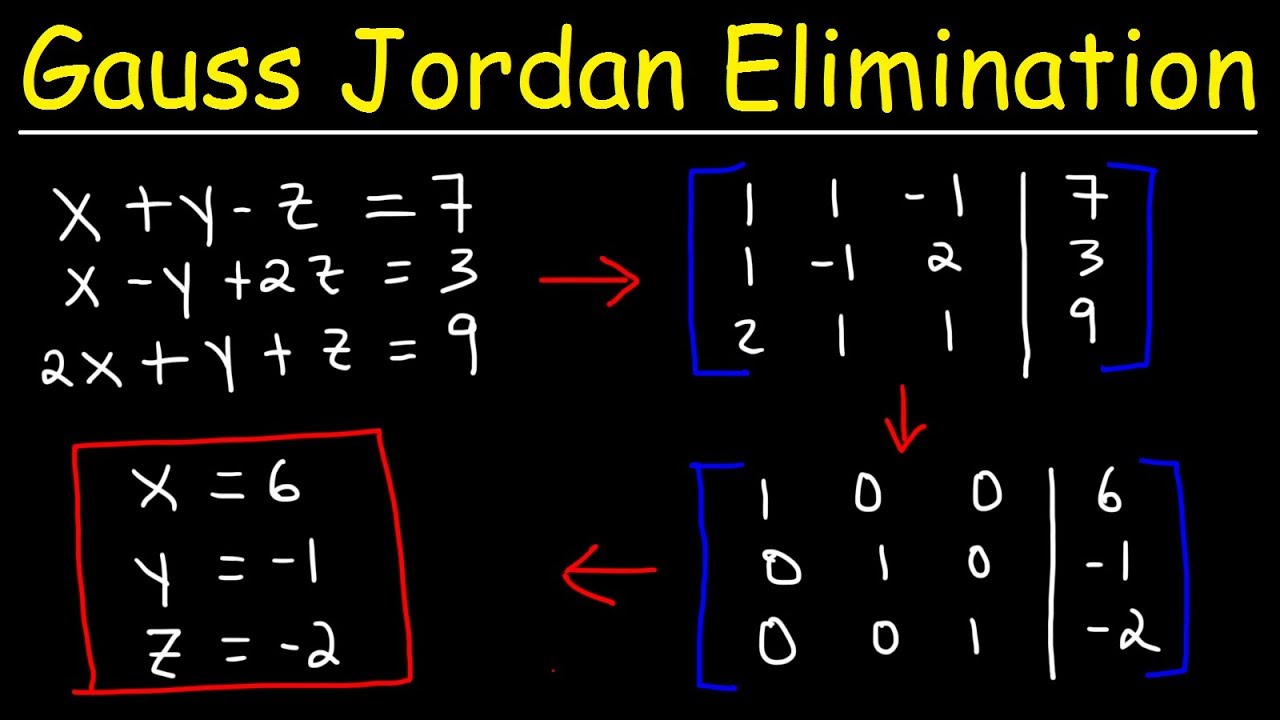
. Both Gauss-Jordan and Gauss elimination are somewhat similar methods the only difference is in the Gauss elimination method the matrix is reduced. Set an augmented matrix. The end product of Gauss Jordan elimination is a matrix in reduced row echelon form.

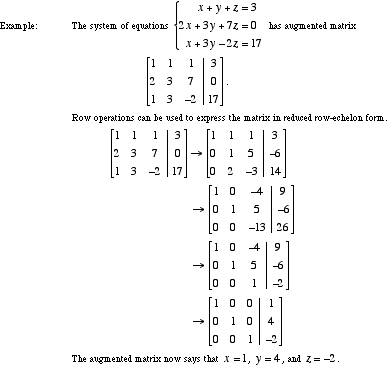
In mathematics Gaussian elimination also known as row reduction is an algorithm for solving systems of linear equations. A matrix is in the reduced row echelon form if the first nonzero entry in each row is a 1 and the columns containing these 1s have all other entries as zeros. Write the augmented matrix of the system.

After performing Gaussian elimination on a matrix the result is in row echelon form while the result after the Gauss-Jordan method is in reduced row echelon form. To solve a system of linear equations using Gauss-Jordan elimination you need to do the following steps. Add a scalar multiple of one row to any.

This completes Gauss Jordan elimination. A The rows if any consisting entirely of zeros. Displays Gaussian elimination steps.

In fact Gauss-Jordan elimination algorithm is divided into forward elimination and back substitution. The Gauss-Jordan elimination algorithm produces from a matrix B a row reduced matrix rrefB. Gauss-Jordan elimination Gauss-Jordan elimination is another method for solving systems of equations in matrix form.

Multiply a row by any non-zero constant. It consists of a sequence of operations performed on the corresponding matrix of coefficients. In this video multiple systems of equations are solved using the Gauss-Jordan Elimination method.

The Formula used by the Gaussian Elimination Method Calculator. In this method the unknowns are eliminated successively and the system is reduced to an upper triangular system from which the unknowns are found by back substitution. Rows that consist of only zeroes are in the bottom of the matrix.

It is really a continuation of Gaussian elimination. If we look. There exist only one difference between both.

Swap the positions of two of the rows. This method can also be used to compute the rank of a matrix the determinant of a square matrix and the. The method of determinants pioneered 1I checked with Ajak who also hinted.

Feel free to pause the video at any step to follow along t. Forward elimination of Gauss-Jordan calculator reduces matrix to row echelon form. The Gauss-Jordan method is similar to the Gaussian elimination process except that the entries both above and below each pivot are zeroed out.

Turn matrix into reduced row-echelon form 𝑏𝑏 1 0 0 0 1 0 0 0 1 𝑎𝑎 𝑐𝑐. There are three elementary row operations used to achieve reduced row echelon form. The best gauss jordan elimination calculator with steps does the following calculations.

The method is named after Carl Friedrich Gauss 17771855 although some special cases of the methodalbeit presented without proofwere known to Chinese mathematicians as early as circa 179 CE. In this method elimination of unknowns is performed by all equations not only from equations to follow. The algorithm allows to do three things.

To convert any matrix to its reduced row echelon form Gauss-Jordan elimination is performed. What is the difference between Gauss elimination and Gauss Jordan method. Gauss Elimination Method Gauss Jordan Method.

The Gauss Jordan Elimination is an algorithm to solve a system of linear equations by representing it as an augmented matrix reducing it using row operations and expressing the system in the reduced row-echelon form to find the solution. Where there the Gauss elimination generates the reduced. Learn more about this method with the help of an example at BYJUS.

This is a n m1 matrix as there are m1 columns now. It relies upon three elementary row operations one can use on a matrix. Subtract a row from another row scale a row and swap two rows.

Let Abe an m nmatrix. Multiply one of the rows by a nonzero scalar. Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix.

A homogeneous linear system is always. Note that if one has a matrix in reduced. The Gauss-Jordan elimination method to solve a system of linear equations is described in the following steps.

Gauss elimination method is used to solve the given system of linear equations by performing a series of row operations. As mentioned earlier the Gauss-Jordan method starts out with an augmented matrix and by a series of row operations ends up with a matrix that is in the reduced row echelon form. We say that Ais in reduced row echelon form if Ain echelon form and in addition every other entry of a column which contains a pivot is zero.

Gauss Jordan Elimination Reduced Row Echelon Form Youtube

Gauss Jordan Elimination Reduced Row Echelon Form Rref Youtube